vollständige Induktion

01

Für alle natürlichen Zahlen sowie und alle nicht-negativen reellen Zahlen ist die Gültigkeit folgender Ungleichung zu beweisen.

03

Durch vollständige Induktion ist für alle natürlichen Zahlen die Gültigkeit folgender Gleichung zu beweisen:

04

Durch vollständige Induktion ist für alle natürlichen Zahlen die Gültigkeit folgender Ungleichung zu beweisen:

05

Durch vollständige Induktion ist für alle natürlichen Zahlen die Gültigkeit folgender Ungleichung zu beweisen:

06

Für alle natürlichen Zahlen ist die Gültigkeit folgender Ungleichung zu beweisen:

07

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung zu beweisen:

09

Sei eine beliebige reelle Zahl. Für alle natürlichen Zahlen ist zu beweisen, dass die folgende Ungleichung gilt.

10

Durch vollständige Induktion ist für alle natürlichen Zahlen und für alle reellen Zahlen a und q die Gültigkeit folgender Gleichung zu beweisen.

11

Durch vollständige Induktion ist für alle natürlichen Zahlen und für alle reellen Zahlen a und die Gültigkeit folgender Gleichung zu beweisen.

14

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung zu beweisen.

15

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung zu beweisen.

18

Für alle natürlichen Zahlen und alle reellen Zahlen a ist die Gültigkeit folgender Gleichung zu beweisen.

19

Für alle natürlichen Zahlen und alle reellen Zahlen a ist die Gültigkeit folgender Gleichung zu beweisen.

24

Für alle natürlichen Zahlen ist die Gültigkeit folgender Ungleichung zu beweisen.

31

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung durch vollständige Induktion zu beweisen.

32

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung durch vollständige Induktion zu beweisen.

59

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung zu beweisen.

60

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung zu beweisen.

64

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung zu beweisen.

65

Für alle natürlichen Zahlen ist die Gültigkeit folgender Gleichung zu beweisen.

75

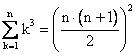
Für alle natürlichen Zahlen ist durch vollständige Induktion die Gleichung zu beweisen .

79

Durch vollständige Induktion ist zu beweisen:

80

Durch vollständige Induktion ist für zu beweisen:

84

Durch vollständige Induktion ist zu beweisen:

85

Durch vollständige Induktion ist zu beweisen:

86

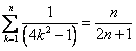
Durch vollständige Induktion und ist zu beweisen:

87

Für alle ist die Gültigkeit folgender Gleichung durch vollständige Induktion zu beweisen.

Hinweis: Der Beweis stützt sich auf Aufgabe 22; vgl. auch Aufgabe 33!

88

Für alle ist die Gültigkeit folgender Gleichung durch vollständige Induktion zu beweisen.

Hinweis: Der Beweis stützt sich auf Aufgabe 22; vgl. auch Aufgabe 34!

89

Für alle ist die Gültigkeit folgender Gleichung zu beweisen

90

Sei fest vorgegeben und für alle gilt zu beweisen: